2021. 7. 22. 00:13ㆍData Science/01_Machine Learning Study
분위수 회귀(Quantile Regression) 소개
: 팀에서 공유 섹션으로 간단한 분위수 회귀(Quantile reg)를 준비
: 발표 내용 중 일부를 코드와 함께 공유하고자 함
1. 분위수 회귀(Quantile Resgression)?
: 분위수 회귀는 선형 회귀 조건이 충족되지 않을 때 사용되는 선형 회귀의 확장 버전
https://ko.wikiqube.net/wiki/Quantile_regression

: 실제로 내가 사용하는 경우는 아래와 같음
1) Robust한 결과를 내고 싶을 때
2) 이상치가 많아 이에 대한 영향을 줄인 선형 회귀선을 구하고 싶을 때
3) 점 추정이 아닌 구간추정을 통해 결과의 정확도를 높이고 싶을 때
4) 반응변수의 스프레드를 같이 살펴보고 싶을 때
5) 선형 회귀 가정이 어려울 때
6) 내 회귀선을 상대방에게 더 설득력 있게 보이고 싶을 때
: 그림과 같이 Reg 문제를 ML/DL로 풀어야 할 때 사용할 수 있음
: 예상도착시간 등에 단순 점 추정이 아닌 구간 추정을 통해 예측 정확도를 다르게 표현이 가능

2. 분위수 회귀(Quantile Regression)의 LossFunction
: 우리가 가장 많이 사용하는 OLS 회귀는 조건부 평균값을 모델링하는 반면 분위수 회귀는 조건부 분위수를 모델링 함
: 조건부 분위수를 모델링하기 위해 Pinball loss를 사용함

: pinball loss의 공식은 처음 봤을 때 복잡해보일 수 있지만 한줄씩 읽어보면 매우 간단함
: 0.5 보다 분위수가 클 경우, 과소 추정에 대한 penalty를 더 부여함
: 0.5 보다 분위수가 작을 경우, 과대 추정에 대한 penalty를 더 부여함

: 결론
분위수 회귀(Quantile Reg)는 반응 변수의 조건부 분위수를 모델링 하는 모델이며 이를 위해 Pinball loss를 사용함
3. 분위수 회귀(Quantile Regression) with Python
: 분위수 회귀는 이미 다양한 API로 구현이 되어 있음
: 가장 많이 사용하는 모델과 RF로 접근하는 방식을 파이썬으로 소개하고자 함
사용한 패키지
from sklearn.datasets import make_regression
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as npfrom sklearn.model_selection
import train_test_splitimport statsmodels.formula.api as smf
from lightgbm import LGBMRegressor
from sklearn.ensemble import RandomForestRegressor
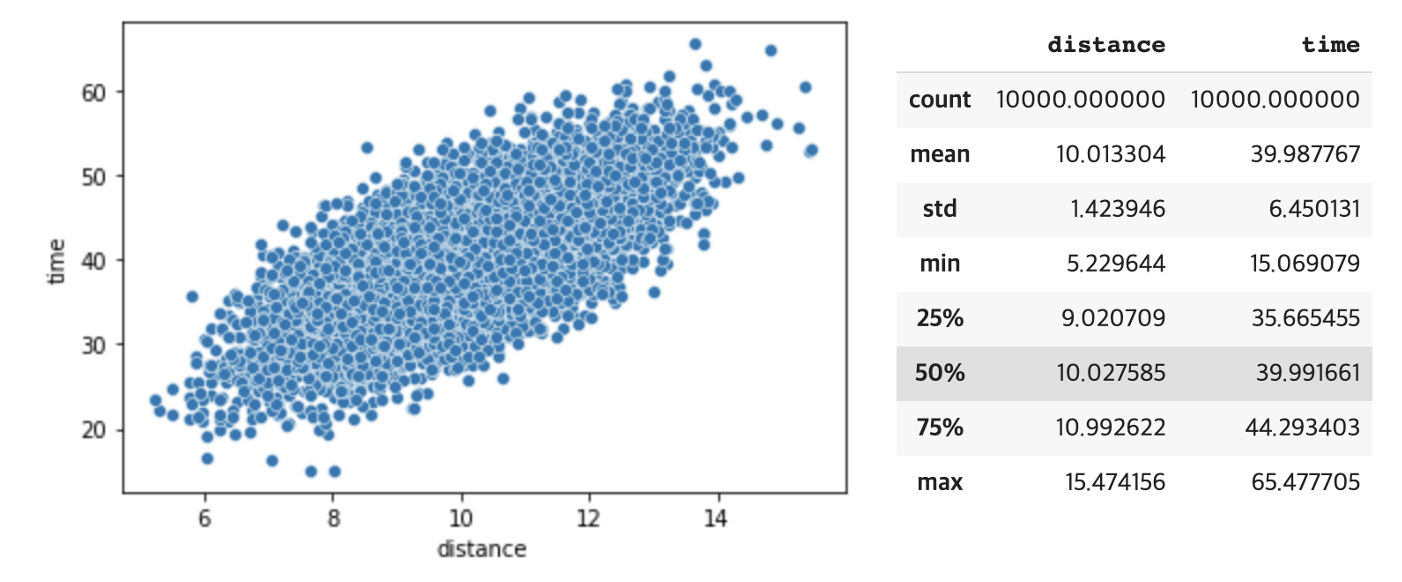
데이터 만들기
x, y = make_regression( n_samples=10000, n_features=1, n_informative=1, n_targets=1, random_state=42 )
df = pd.DataFrame([x.reshape(-1), y.reshape(-1)]).T
df.columns = ['distance', 'time']
df['distance'] = df['distance'].apply(lambda x: 10 + (x +np.random.normal()))
df['time'] = df['time'].apply(lambda x: 40 + 0.2 * (x +np.random.normal()))
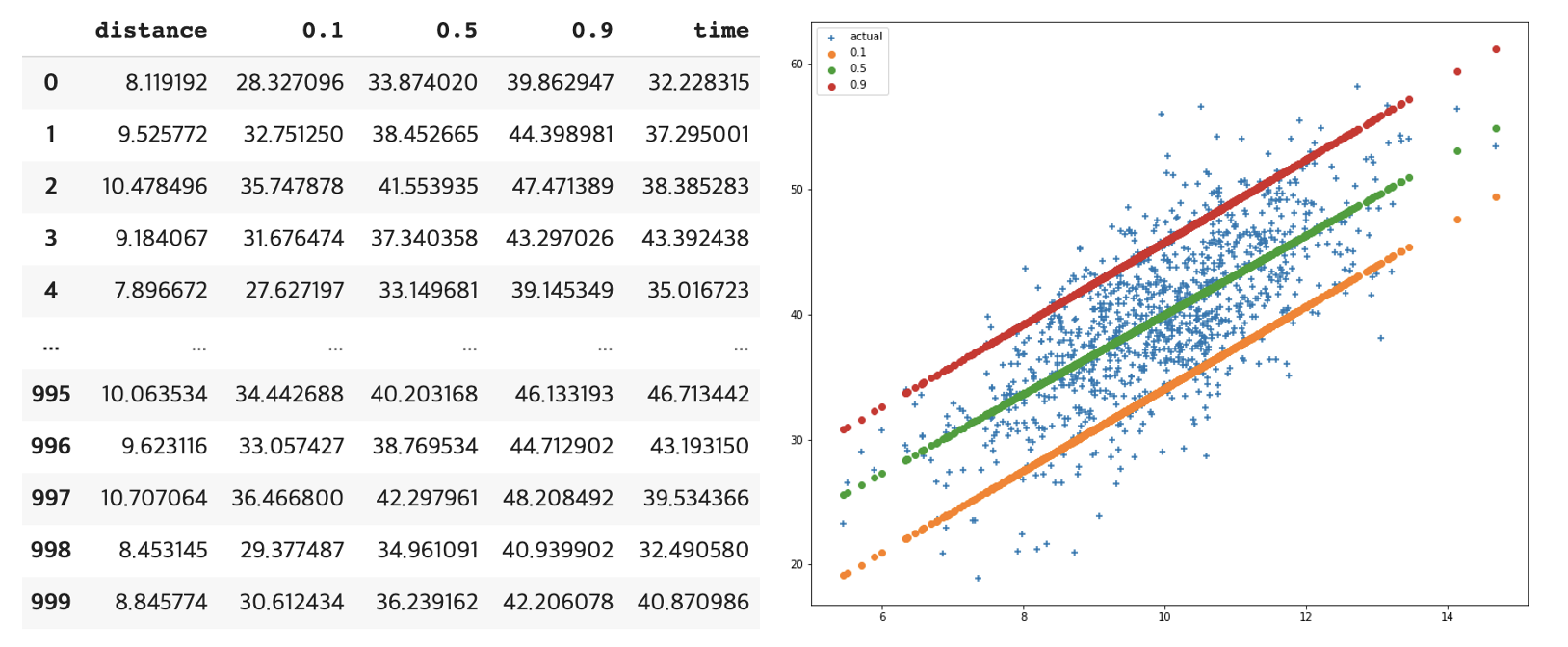
1) Stats Model_Quantile Reg
train_x, test_x, train_y ,test_y = train_test_split( df[['distance']], df[['time']], test_size=0.1, random_state=42, )
print(train_x.shape)
print(train_y.shape)
print(test_x.shape)
print(test_y.shape)
model_list = []
pred_dict = {}
for quantile in [0.1, 0.5, 0.9]:
df = pd.concat([train_x, train_y], axis=1).reset_index(drop=True)
quantile_reg = smf.quantreg('time ~ distance', df).fit(q = quantile)
pred = quantile_reg.predict(test_x)
pred_dict[quantile] = pred
pred_df = pd.concat(
[test_x.reset_index(drop=True),
pd.DataFrame(pred_dict).reset_index(drop=True),
test_y.reset_index(drop=True)],
axis=1,
)
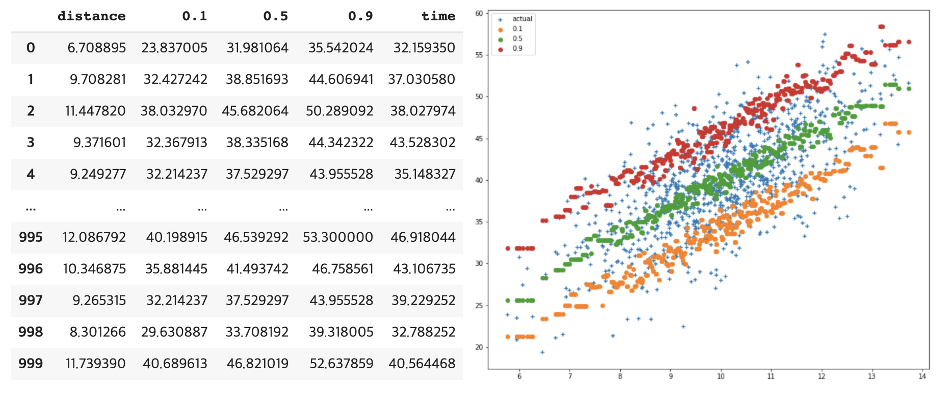
2) LGBM_Quantile Reg
train_x, test_x, train_y ,test_y = train_test_split( df[['distance']], df[['time']], test_size=0.1, random_state=42, )
print(train_x.shape)
print(train_y.shape)
print(test_x.shape)
print(test_y.shape)
model_list = []
pred_dict = {}
for quantile in [0.1, 0.5, 0.9]:
clf = LGBMRegressor(objective = 'quantile', alpha = quantile)
clf.fit(train_x, train_y)
pred = clf.predict(test_x)
pred_dict[quantile] = pred
pred_df = pd.concat(
[test_x.reset_index(drop=True),
pd.DataFrame(pred_dict).reset_index(drop=True),
test_y.reset_index(drop=True)],
axis=1,
)
3) RF_Quantile Reg 접근 방법
for i in range(10):
df['x_{}'.format(i)] = df['distance'].apply(lambda x: (i+10) * 5 + (x +np.random.normal()))
train_x, test_x, train_y ,test_y = train_test_split( df[['distance']], df[['time']], test_size=0.1, random_state=42, )
print(train_x.shape)
print(train_y.shape)
print(test_x.shape)
print(test_y.shape)
model_list = []
pred_dict = {}
rf = RandomForestRegressor( n_estimators=1000, random_state=42, n_jobs=-1 )
rf.fit(train_x.values, train_y.values)
for estimator in rf.estimators_:
pred_list.append(estimator.predict(test_x))
for quantile in [0.1, 0.5, 0.9]:
y_pred = np.percentile(pred_list, quantile * 100, axis=0)
pred_dict[quantile] = y_pred
pred_df = pd.concat(
[test_x.reset_index(drop=True),
pd.DataFrame(pred_dict).reset_index(drop=True),
test_y.reset_index(drop=True)],
axis=1,
)
'Data Science > 01_Machine Learning Study' 카테고리의 다른 글
| 파이토치 허브(PYTORCH HUB) (0) | 2022.07.13 |
|---|---|
| 단순회귀모형_단순회귀분석(2/2부) (0) | 2021.03.14 |
| 단순회귀모형_단순회귀분석(1/2부) (0) | 2021.03.10 |
| Prophet을 활용한 Kaggle 문제 풀어보기 (0) | 2021.02.25 |
| Auto ML PyCaret을 활용한 Kaggle 문제 풀기 (0) | 2020.10.04 |