2023. 1. 1. 22:46ㆍData Science/05_Research paper

long-term time series forecasting (LTSF) 과제에서 Informer와 같이 Transformer 기반 모델이 실제로 효과적인지 살펴보고 간단한 선형 및 분해 모델로도 높은 성능을 낼 수 있다는 LTSF-Linear: Are Transformers Effective for Time Series Forecasting? 논문을 소개하고자 합니다.
CONCEPT
본 논문은 트랜스포머 모델이 명확한 추세와 주기성을 지닌 장기 시계열 예측에 정말 효과적인가에 대한 질문으로부터 시작합니다.

LTSF 과제에서는 시간적 변화를 모델링하는데 주 목적을 두기 때문에 시간 순차성 정보가 예측에 있어 가장 중요한 역할을 하게 됩니다. 트랜스포머의 경우 이런 시간 순차성 정보를 보존하기 위해 위치 positional encoding 기법을 사용하였지만 인코딩하는 과정과 다음에 진행되는 multi-head self-attention 적용 후 시간 순차성에 대한 정보 손실을 피할 수는 없습니다. 일반적으로 트랜스포머 모델이 주로 사용되는 NLP 분야에서는 문장 내 단어의 순서가 어느 정도 바뀌어도 의미 자체가 크게 변하지 않기 때문에(ex. 나는 배가 고프다, 배가 고프다 나는) 큰 문제가 발생하지 않지만, 추세와 주기성을 지닌 수치 시계열 데이터에서는 의미 정보가 부족하기 때문에 이와 같은 정보 손실은 큰 문제를 야기시킬 수 있습니다. 실제로 트랜스포머 모델의 경우 look-back window sizes를 증가시켜도 예측 오류가 감소(때로는 증가)하지 않는 현상을 보고 시간적인 관계에 대한 특징을 추출하지 못한다는 것을 발견했습니다. 그렇기 때문에 LTSF 벤치마크 과제에서 트랜스포머 모델의 성능이 다소 과장되었다고 생각되며 장기 시계열 예측에 정말 효과적인가에 대한 의문이 시작됐습니다.

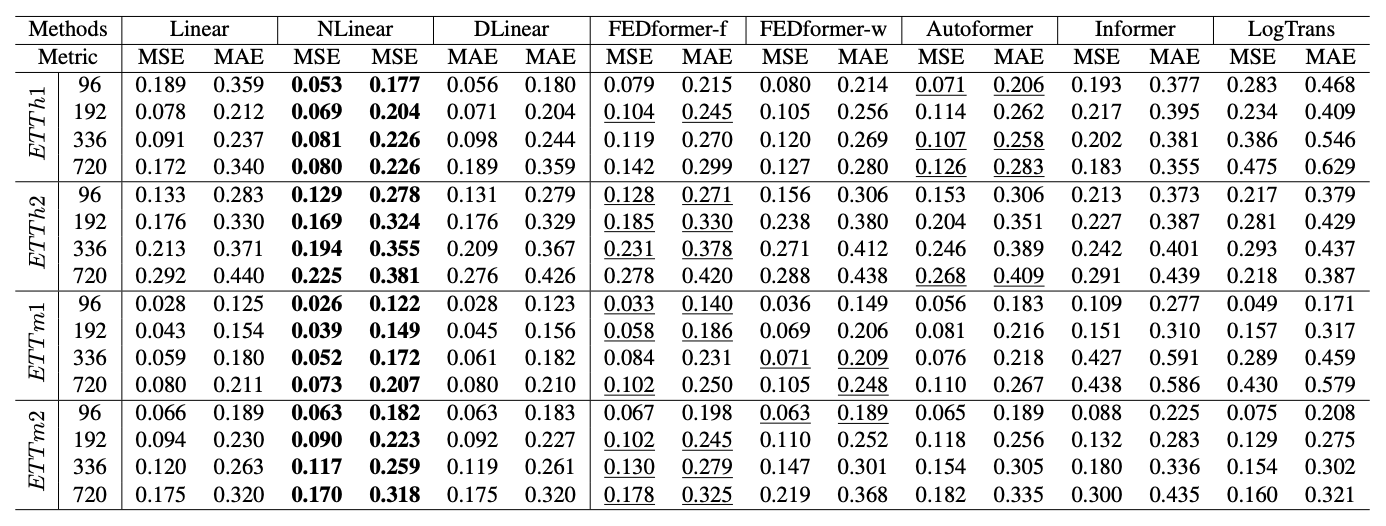
위와 같은 이유로 본 논문에서는 간단한 선형 모델이 장기 시계열 데이터에서 시간 순차성 정보를 그대로 보존하면서 추세와 주기성에 대한 특징을 보다 잘 추출할 수 있기 때문에 LTSF-Linear 모델을 제안했습니다. 해당 모델은 간단한 단일 선형 레이어로 구성되었지만 9개의 벤치마크 데이터셋에서 기전의 트랜스포머 기반 모델보다 뛰어난 성능을 보여줬습니다.

STRUCTURE
3개의 LTSF-Linear 모델을 코드와 함께 설명해드리겠습니다.
(1) Linear
- Linear: 단 하나의 선형 레이어로 구성된 모델이지만 트랜스포머 모델보다 성능이 우수합니다.

class LTSF_Linear(torch.nn.Module):
def __init__(self, window_size, forcast_size, individual, feature_size):
super(LTSF_Linear, self).__init__()
self.window_size = window_size
self.forcast_size = forcast_size
self.individual = individual
self.channels = feature_size
if self.individual:
self.Linear = torch.nn.ModuleList()
for i in range(self.channels):
self.Linear.append(torch.nn.Linear(self.window_size, self.forcast_size))
else:
self.Linear = torch.nn.Linear(self.window_size, self.forcast_size)
def forward(self, x):
if self.individual:
output = torch.zeros([x.size(0), self.forcast_size, x.size(2)],dtype=x.dtype).to(x.device)
for i in range(self.channels):
output[:,:,i] = self.Linear[i](x[:,:,i])
x = output
else:
x = self.Linear(x.permute(0,2,1)).permute(0,2,1)
return x
(2) DLinear
- DLinear: 이 모델은 Autoformer와 FEDformer에서 사용되는 시계열 분해 방식을 선형 레이어와 결합한 모델입니다. 먼저 이동 평균값을 만들고 이를 제거하여 각각 학습하기 위해 추세와 주기성 데이터로 분해합니다. 그런 다음 각 구성 요소에 단일 선형 레이어를 적용하여 학습하고 두 개를 합산하여 최종 예측을 계산합니다. Dlinear는 시계열 데이터의 명확한 추세와 주기성이 있을 때 바닐라 선형 모델보다 더 나은 성능을 가질 수 있습니다.

class moving_avg(torch.nn.Module):
def __init__(self, kernel_size, stride):
super(moving_avg, self).__init__()
self.kernel_size = kernel_size
self.avg = torch.nn.AvgPool1d(kernel_size=kernel_size, stride=stride, padding=0)
def forward(self, x):
front = x[:, 0:1, :].repeat(1, (self.kernel_size - 1) // 2, 1)
end = x[:, -1:, :].repeat(1, (self.kernel_size - 1) // 2, 1)
x = torch.cat([front, x, end], dim=1)
x = self.avg(x.permute(0, 2, 1))
x = x.permute(0, 2, 1)
return x
class series_decomp(torch.nn.Module):
def __init__(self, kernel_size):
super(series_decomp, self).__init__()
self.moving_avg = moving_avg(kernel_size, stride=1)
def forward(self, x):
moving_mean = self.moving_avg(x)
residual = x - moving_mean
return moving_mean, residual
class LTSF_DLinear(torch.nn.Module):
def __init__(self, window_size, forcast_size, kernel_size, individual, feature_size):
super(LTSF_DLinear, self).__init__()
self.window_size = window_size
self.forcast_size = forcast_size
self.decompsition = series_decomp(kernel_size)
self.individual = individual
self.channels = feature_size
if self.individual:
self.Linear_Seasonal = torch.nn.ModuleList()
self.Linear_Trend = torch.nn.ModuleList()
for i in range(self.channels):
self.Linear_Trend.append(torch.nn.Linear(self.window_size, self.forcast_size))
self.Linear_Trend[i].weight = torch.nn.Parameter((1/self.window_size)*torch.ones([self.forcast_size, self.window_size]))
self.Linear_Seasonal.append(torch.nn.Linear(self.window_size, self.forcast_size))
self.Linear_Seasonal[i].weight = torch.nn.Parameter((1/self.window_size)*torch.ones([self.forcast_size, self.window_size]))
else:
self.Linear_Trend = torch.nn.Linear(self.window_size, self.forcast_size)
self.Linear_Trend.weight = torch.nn.Parameter((1/self.window_size)*torch.ones([self.forcast_size, self.window_size]))
self.Linear_Seasonal = torch.nn.Linear(self.window_size, self.forcast_size)
self.Linear_Seasonal.weight = torch.nn.Parameter((1/self.window_size)*torch.ones([self.forcast_size, self.window_size]))
def forward(self, x):
trend_init, seasonal_init = self.decompsition(x)
trend_init, seasonal_init = trend_init.permute(0,2,1), seasonal_init.permute(0,2,1)
if self.individual:
trend_output = torch.zeros([trend_init.size(0), trend_init.size(1), self.forcast_size], dtype=trend_init.dtype).to(trend_init.device)
seasonal_output = torch.zeros([seasonal_init.size(0), seasonal_init.size(1), self.forcast_size], dtype=seasonal_init.dtype).to(seasonal_init.device)
for idx in range(self.channels):
trend_output[:, idx, :] = self.Linear_Trend[idx](trend_init[:, idx, :])
seasonal_output[:, idx, :] = self.Linear_Seasonal[idx](seasonal_init[:, idx, :])
else:
trend_output = self.Linear_Trend(trend_init)
seasonal_output = self.Linear_Seasonal(seasonal_init)
x = seasonal_output + trend_output
return x.permute(0,2,1)
(3) NLinear
- NLinear: 상승하거나 하락하는 추세를 지녔을 경우 학습 데이터의 평균과 분산으로 데이터를 정규화시키면 평가 데이터에 분포 이동이 발생할 수 있습니다. 이럴 경우 학습된 모형의 예측 값은 분포에서 크게 벗어나기 때문에 예측 성능이 하락하게 됩니다. 따라서 NLinear 모델을 이를 개선하기 위해 가장 마지막 값을 빼서 모델을 학습시키고 가장 마지막에 다시 그 값을 더해서 실제 값이 존재하는 분포로 이동시킵니다. 이와 같은 학습 데이터와 평가 데이터의 분포 차이는 ETth1, ETth2, ILI 벤치마크 데이터셋에서 관찰되었고 실험결과 높은 성능을 보여줬다는 것을 증명했습니다.

class LTSF_NLinear(torch.nn.Module):
def __init__(self, window_size, forcast_size, individual, feature_size):
super(LTSF_NLinear, self).__init__()
self.window_size = window_size
self.forcast_size = forcast_size
self.individual = individual
self.channels = feature_size
if self.individual:
self.Linear = torch.nn.ModuleList()
for i in range(self.channels):
self.Linear.append(torch.nn.Linear(self.window_size, self.forcast_size))
else:
self.Linear = torch.nn.Linear(self.window_size, self.forcast_size)
def forward(self, x):
seq_last = x[:,-1:,:].detach()
x = x - seq_last
if self.individual:
output = torch.zeros([x.size(0), self.forcast_size, x.size(2)],dtype=x.dtype).to(x.device)
for i in range(self.channels):
output[:,:,i] = self.Linear[i](x[:,:,i])
x = output
else:
x = self.Linear(x.permute(0,2,1)).permute(0,2,1)
x = x + seq_last
return x
해당 논문에서 소개되는 모델들은 기존 트랜스포머 모델들에 비해 굉장히 간단하지만 벤치마크 데이터셋에서 보다 우수한 성능을 보여주었습니다. 실제 대회 데이터를 바탕으로 실험하였을 때도 기존 트랜스포머 모델보다 높은 성능을 보여주는지, 논문에서 설명한 대로 추세, 주기성 특징에 따라 모델 성능이 개선되는지 살펴보도록 하겠습니다.
EXAMPLE
데이콘에서 열렸던 전력사용량 예측 AI 경진대회 데이터를 사용해서 모델 성능을 비교해 보겠습니다.
https://dacon.io/competitions/official/235736/data
전력사용량 예측 AI 경진대회 - DACON
분석시각화 대회 코드 공유 게시물은 내용 확인 후 좋아요(투표) 가능합니다.
dacon.io
데이터를 살펴보면 20-6-1부터 20-8-24일 까지 약 3달간 총 60개 건물 시간대별 전력사용량 및 기상정보에 대한 데이터를 제공하고 있습니다. 60개 모든 건물을 비교하기 전에 추세와 주기성을 명확하게 지닌 건물 1개를 지정하여 살펴보도록 하겠습니다.
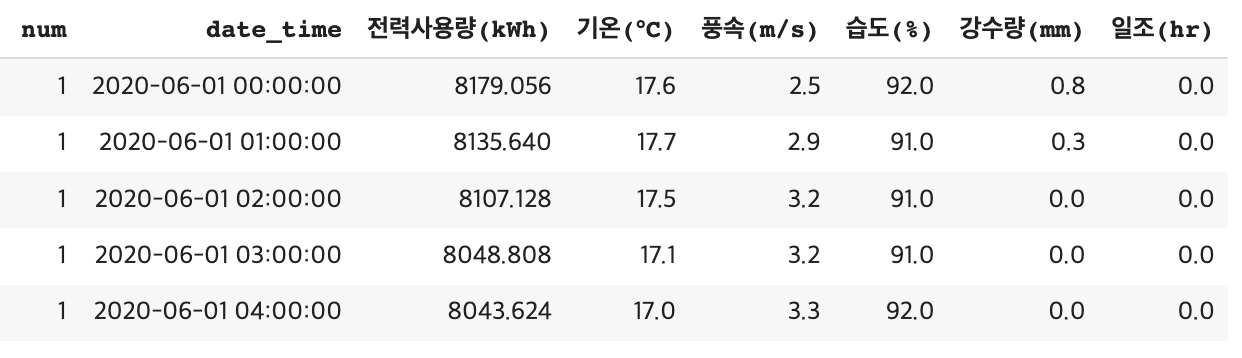
5번 건물의 전력 사용량을 보면 다소 증가하는 추세와 하루 단위의 주기성을 보여주고 있습니다. 해당 데이터에서 학습/평가/실험 데이터를 분리하여 성능일 비교해 보겠습니다.
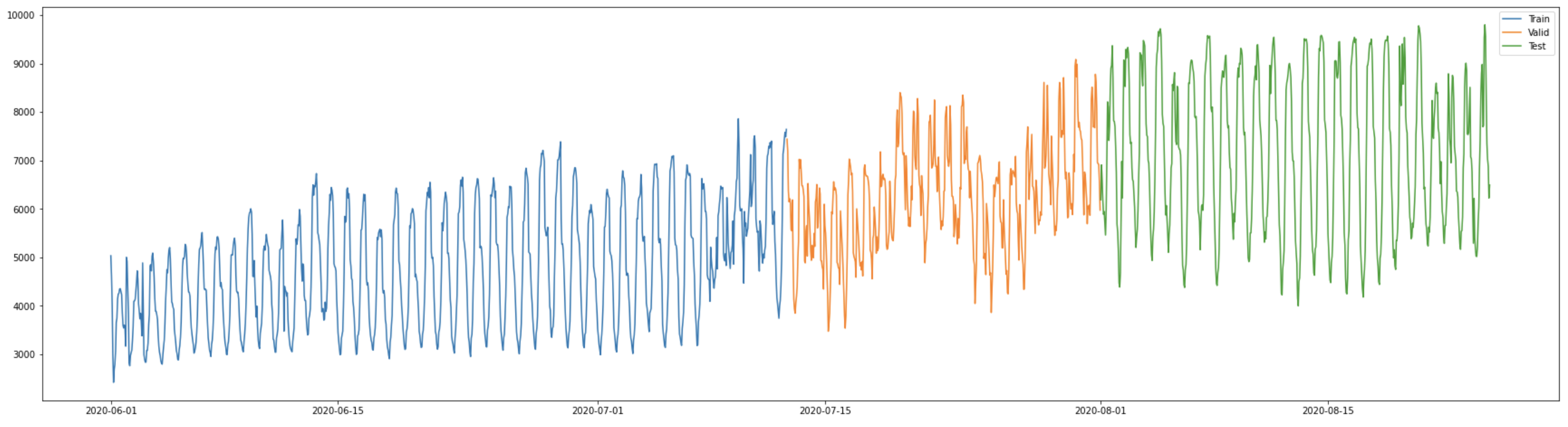
사용할 모델은 총 4개로 바닐라 트랜스포머, Linear, DLinear, NLinear입니다. 학습 데이터 전처리의 경우 정규화와 Sliding Window를 진행했으며 파라미터는 window size=72, Forcast size=24, Batch size=32, lr=1e-4, loss=MSE, opt=Adam을 사용했으며 평가 데이터 기준 가장 높은 성능의 모델을 저장하여 실험을 진행했습니다.
def standardization(train_df, test_df, not_col, target):
train_df_ = train_df.copy()
test_df_ = test_df.copy()
col = [col for col in list(train_df.columns) if col not in [not_col]]
mean_list = []
std_list = []
for x in col:
mean, std = train_df_.agg(["mean", "std"]).loc[:,x]
mean_list.append(mean)
std_list.append(std)
train_df_.loc[:, x] = (train_df_[x] - mean) / std
test_df_.loc[:, x] = (test_df_[x] - mean) / std
return train_df_, test_df_, mean_list[col.index(target)], std_list[col.index(target)]
def time_slide_df(df, window_size, forcast_size, date, target):
df_ = df.copy()
data_list = []
dap_list = []
date_list = []
for idx in range(0, df_.shape[0]-window_size-forcast_size+1):
x = df_.loc[idx:idx+window_size-1, target].values.reshape(window_size, 1)
y = df_.loc[idx+window_size:idx+window_size+forcast_size-1, target].values
date_ = df_.loc[idx+window_size:idx+window_size+forcast_size-1, date].values
data_list.append(x)
dap_list.append(y)
date_list.append(date_)
return np.array(data_list, dtype='float32'), np.array(dap_list, dtype='float32'), np.array(date_list)
class Data(Dataset):
def __init__(self, X, Y):
self.X = X
self.Y = Y
def __len__(self):
return len(self.Y)
def __getitem__(self, idx):
return self.X[idx], self.Y[idx]
### Univariable ###
### 데이터 셋 생성 ###
window_size = 72
forcast_size= 24
batch_size = 32
targets = '전력사용량(kWh)'
date = 'date_time'
train_df_fe, test_df_fe, mean_, std_ = standardization(train_df, test_df, 'date_time', targets)
train_x, train_y, train_date = time_slide_df(train_df_fe, window_size, forcast_size, date, targets)
test_x, test_y, test_date = time_slide_df(test_df_fe, window_size, forcast_size, date, targets)
train_ds = Data(train_x[:1000], train_y[:1000])
valid_ds = Data(train_x[1000:], train_y[1000:])
test_ds = Data(test_x, test_y)
train_dl = DataLoader(train_ds, batch_size = batch_size, shuffle=True,)
valid_dl = DataLoader(valid_ds, batch_size = train_x[1000:].shape[0], shuffle=False)
test_dl = DataLoader(test_ds, batch_size = test_x.shape[0], shuffle=False)
### 모델 학습 ###
train_loss_list = []
valid_loss_list = []
test_loss_list = []
epoch = 50
lr = 0.001
DLinear_model = LTSF_DLinear(
window_size=window_size,
forcast_size=forcast_size,
kernel_size=25,
individual=False,
feature_size=1,
)
criterion = torch.nn.MSELoss()
optimizer = torch.optim.Adam(DLinear_model.parameters(), lr=lr)
max_loss = 999999999
for epoch in tqdm(range(1, epoch+1)):
loss_list = []
DLinear_model.train()
for batch_idx, (data, target) in enumerate(train_dl):
optimizer.zero_grad()
output = DLinear_model(data)
loss = criterion(output, target.unsqueeze(-1))
loss.backward()
optimizer.step()
loss_list.append(loss.item())
train_loss_list.append(np.mean(loss_list))
DLinear_model.eval()
with torch.no_grad():
for data, target in valid_dl:
output = DLinear_model(data)
valid_loss = criterion(output, target.unsqueeze(-1))
valid_loss_list.append(valid_loss)
for data, target in test_dl:
output = DLinear_model(data)
test_loss = criterion(output, target.unsqueeze(-1))
test_loss_list.append(test_loss)
if valid_loss < max_loss:
torch.save(DLinear_model, 'DLinear_model.pth')
max_loss = valid_loss
print("valid_loss={:.3f}, test_los{:.3f}, Model Save".format(valid_loss, test_loss))
dlinear_best_epoch = epoch
dlinear_best_train_loss = np.mean(loss_list)
dlinear_best_valid_loss = np.mean(valid_loss.item())
dlinear_best_test_loss = np.mean(test_loss.item())
print("epoch = {}, train_loss : {:.3f}, valid_loss : {:.3f}, test_loss : {:.3f}".format(epoch, np.mean(loss_list), valid_loss, test_loss))
실험 결과 NLinear > DLinear > Linear > Transformer 모델 순으로 나타났습니다. 학습 오류를 살펴보면 4개 모델다 학습에 대한 깊이는 유사하지만 학습/평가/실험 데이터의 평균과 분산이 서로 다르다 보니 바닐라 트랜스포머의 성능이 가장 낮은 걸 확인할 수 있었습니다. 그리고 DLinear의 경우 추세와 주기성 가중치를 직접 살펴볼 수 있었기 때문에 이를 시각화한 자료를 같이 살펴봤습니다. 주기성 가중치를 살펴봤을 때 60~70 timestep이 가장 높은 것을 보아 가장 최근 전력 사용량이 예측에 가장 중요한 것을 볼 수 있었고 주기성 가중치를 살펴보면 24시간 하루를 기준으로 매칭이 되는 전날 동일 시간대가 예측에 가장 중요한 요인이었다는 것을 확인할 수 있었습니다.
weights_list = {}
weights_list['trend'] = DLinear_model.Linear_Trend.weight.detach().numpy()
weights_list['seasonal'] = DLinear_model.Linear_Seasonal.weight.detach().numpy()
for name, w in weights_list.items():
fig, ax = plt.subplots()
plt.title(name)
im = ax.imshow(w, cmap='plasma_r',)
fig.colorbar(im, pad=0.03)
plt.show()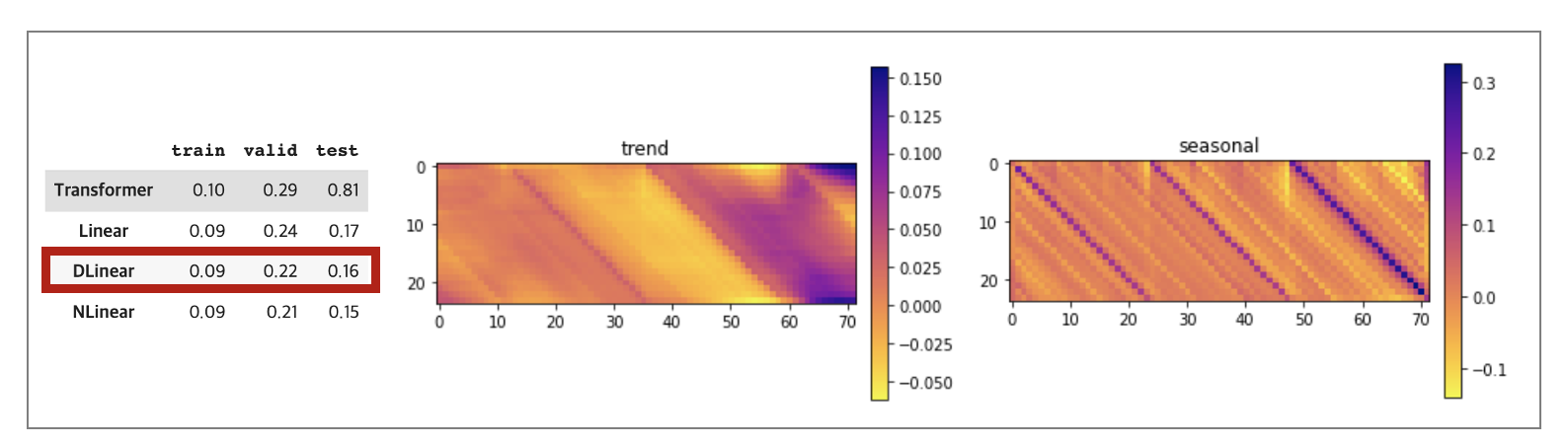
성능 지표뿐만 아니라 실제 예측을 어떻게 했는지 모델별로 비교해보기 위해 랜덤 한 9개 포인트에 대해서 4개 모델의 예측값과 실제 값을 시각화하여 살펴봤습니다. 이에 3개 Linear 모델들은 추세와 주기성을 잘 학습한 것을 눈으로 확인할 수 있었고 이와 반대로 트랜스포머 모델의 경우 스케일을 맞추지 못한 점에서 추세를 반영하지 못했다는 점과 시간 흐름에 따른 변화를 못 따라가는 것을 통해 주기성 또한 제대로 학습하지 못한 것을 볼 수 있었습니다.
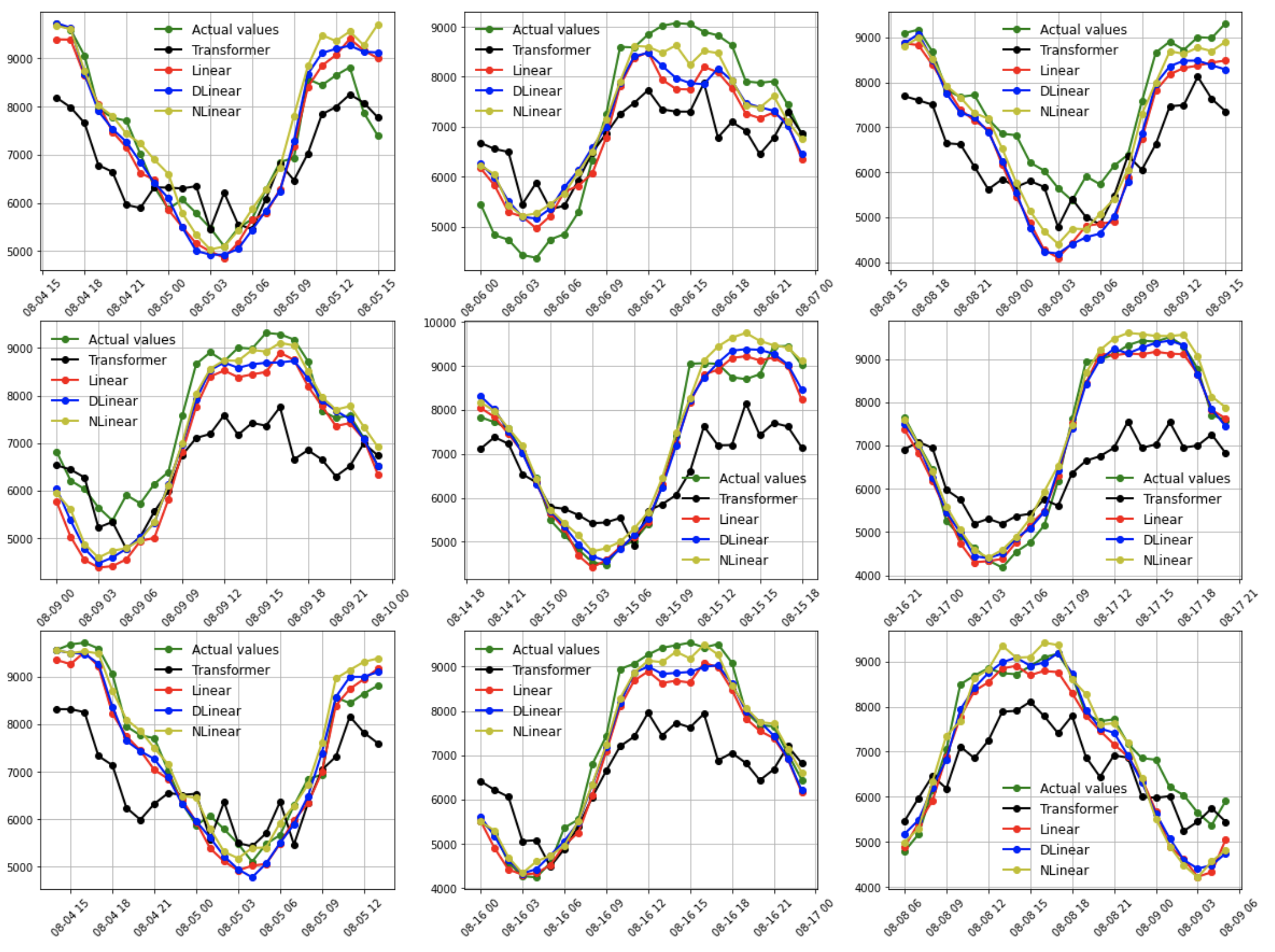
LESSONS LEARNED
"필요 없이 복잡하게 만들지 말 것(Pluralitas non est ponenda sine neccesitate)"
어떠한 현상이나 원리를 나타내기 위한 논리구조에서 쓸모없는 비약, 전제, 논거들을 잘라내는 선택의 방법을 나타내는 용어입니다. 장기 시계열 예측 분야에서도 굳이 복잡도가 높은 트랜스포머 구조를 고집할 필요는 없습니다. 논문에서 소개하는 구조는 직관적이고 간결하기 때문에 앞으로 다양한 환경에 대입하면서 결과를 살펴보고 실험을 설계하면서 발전시켜나가야겠습니다.
'Data Science > 05_Research paper' 카테고리의 다른 글
| TabNet 논문 리뷰(Attentive Interpretable Tabular Learning) (0) | 2022.01.29 |
|---|---|
| Generative Adversarial Nets_GAN_CODE (0) | 2021.03.02 |
| Generative Adversarial Nets_GAN_Overview (0) | 2021.03.02 |