2022. 2. 13. 17:27ㆍData Science/02_Time Series Analysis
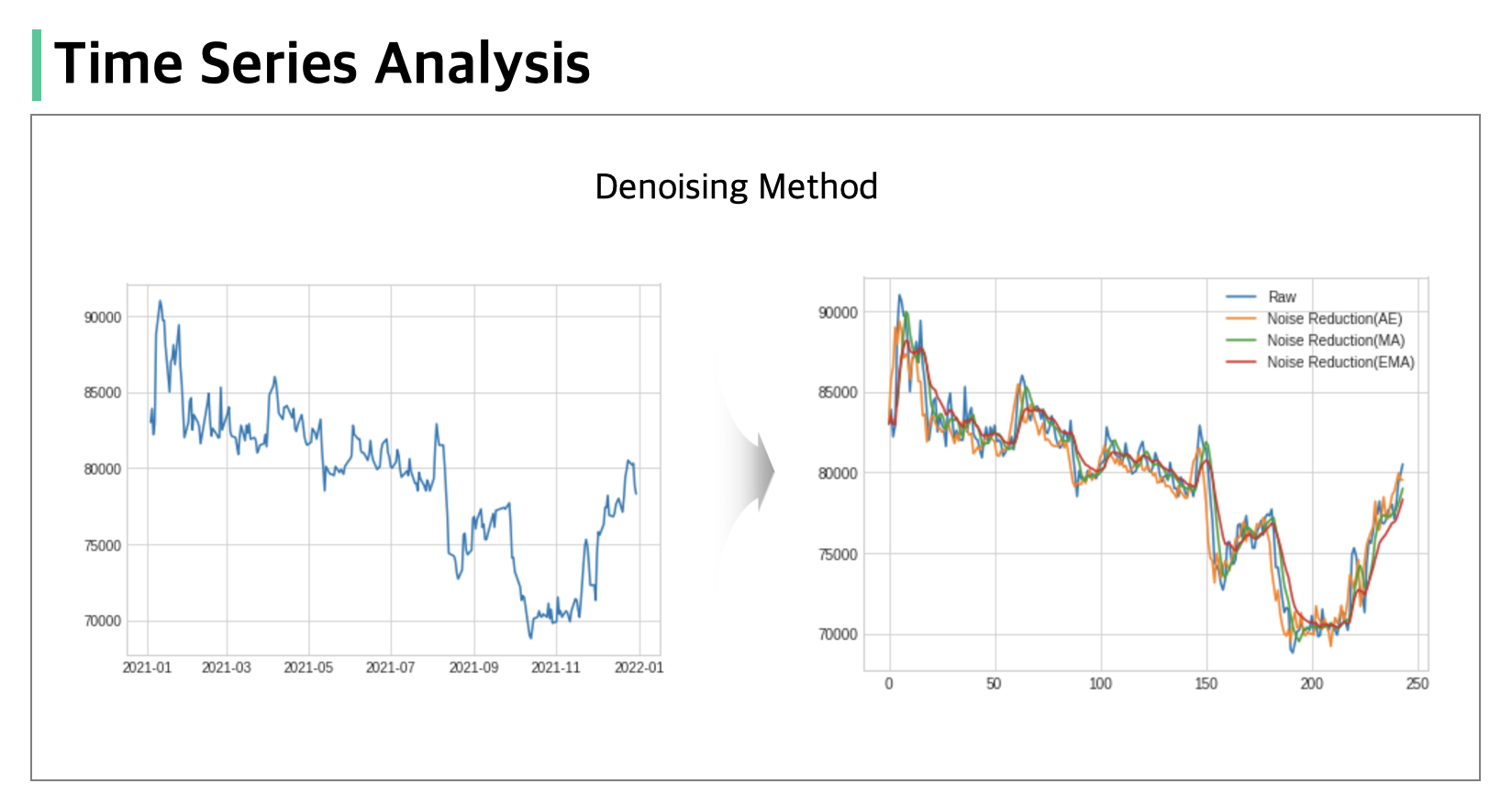
시계열 데이터를 분석하는 과정에서 시간 흐름에 따라 변동이 크거나 일정하지 않을 경우 비정상성(Non-Stationarity)을 지니게 되고 이를 전처리 없이 머신러닝 알고리즘에 학습할 경우 단순 후행 예측, 성능 저하, 잘못된 추론 등의 문제를 야기시킬 수 있습니다.
TIME SERIES FEATURES
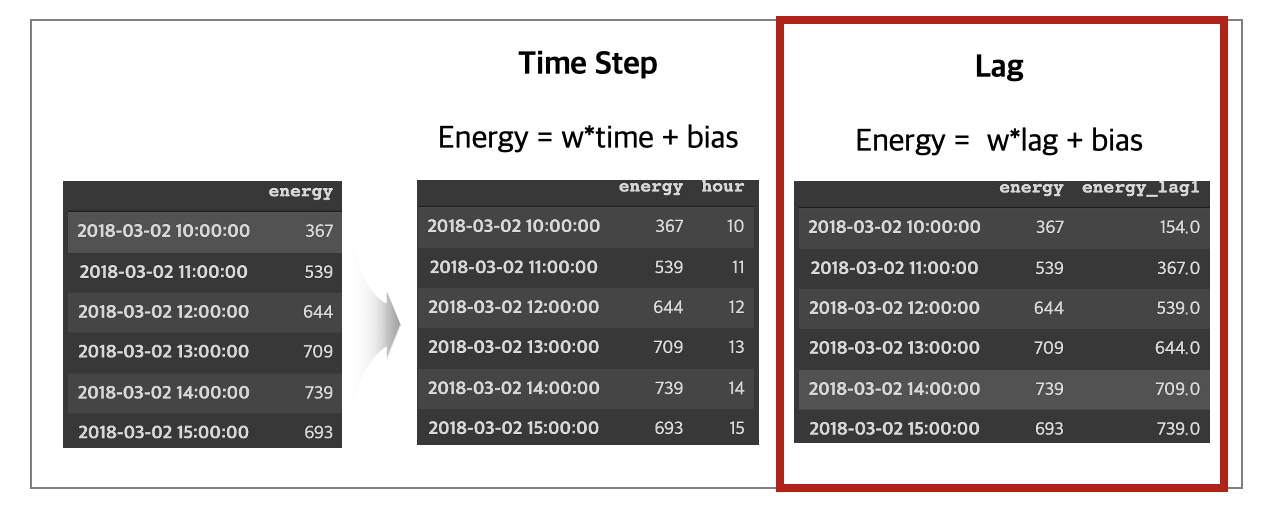
시계열 데이터에는 일반적으로 시간 순차성(Time Step)과 지연 값(Lag)이라는 고유한 2가지 특성이 존재합니다. 두 특성 모두 시간 축을 바탕으로 발생하며 시계열 문제를 머신러닝 모델로 접근하고 해결하기 위해 유용한 특성입니다. 첫 번째, 시간 순차성(Time Step)은 시간축에서 직접 추출 가능하며 시작부터 끝가지 일정 시간 간격으로 측정된 년, 월, 일, 시간 특성이 대표적입니다. 이는 관측값이 주기적 성질을 지니고 있을 때 유용한 특성입니다. 두 번째, 지연 값(Lag)은 관측값에 시간 차이로 발생되며 현재 관측값들은 이전 관측값들로 표현됩니다. 이는 관측값이 자기 상관(AutoCorrelation) 또는 계열 상관성(SerialCorrelation)을 지니고 있을 때 유용한 특성입니다.
이번 포스트에서는 대표적으로 자기 상관(AutoCorrelation) 특성이 강한 금융 시계열 데이터에서 잡음(Noise)을 제거하고 추론에 도움이 되는 정보(Information)를 학습하기 위한 방법을 설명하겠습니다.
WHAT IS AUTOCORRELATION
자기 상관(AutoCorrelation)은 현재 관측값과 지연(Lag) 값들과의 관계에서 발생되는 대표적 요인 중 하나입니다. 해당 특성은 과거 관측된 값들이 미래 관측값에 영향을 지속적으로 미치기 때문에 관측값들의 관계를 우선적으로 파악하고 올바르게 처치해야 원하는 목적에 맞게 데이터를 활용할 수 있습니다. 관계성을 파악하기 위해 ACF/PACF 등을 사용하여 직관적으로 알아보거나 Durbin-Watson 검정을 통해 객관적으로 살펴볼 수 있습니다.
예제로 가져온 주식 종가 데이터를 ACF/PACF로 살펴보니 AR(1)의 특성을 보이고 있습니다. 금융 공학에서는 기하 브라운운동(GBM)을 가정하여 주식 종가 예측 모형을 진행하는데 AR(1)과 근본적으로는 유사하기 때문에 이를 바탕으로 모형을 변형하여 표현할 수 있습니다. 변형된 AR(1) 공식을 살펴보면 다음 주식 종가(t+1)는 현재 주식 종가(t) + 정보(t) + 잡음(t)으로 구성되어 있고 현재 주식 종가(t)를 좌변으로 옮기면 정보(t)와 잡음(t)을 살펴볼 수 있습니다.

시간에 따른 정보(Information)와 잡음(Noise)을 살펴보면 규칙성이 없고 분산이 일정하지 않습니다. 등분산성이 가정되지 않는다면 비정상 시계열이라 표현되며 이때 잡음(Noise)이 정보(Information)에 비해 상대적으로 더 큰 영향을 미치게 됩니다. 이로 인해 좋은 정보량을 잡음으로 인해 잃게 되고 다음 종가(t+1)는 현재 종가(t)와 잡음(t)으로 구성된 것처럼 설명되기에 예측 모델이 잔차를 최소화하기 위해 후행 예측을 야기하게 됩니다.

잡음(Noise)은 기존 신호의 간섭뿐만 아니라 여러 가지 의도치 않은 신호의 왜곡을 불러일으킬 수 있습니다. 그렇기 때문에 머신러닝 모델이 신호를 잘 이해하고 올바른 패턴을 학습시키기 위해 잡음 제거(Denoise)하는 데이터 전처리가 필요합니다.
TIME SERIES DENOISING
시계열 데이터에서 잡음 제거(Denoising) 방법으로 추세를 살펴볼 때 사용하는 이동평균선(Moving-Average)부터 시작하여 쌍방 필터(Bilateral Filter), 딥러닝을 활용한 잡음 제거 방식까지 예제 데이터를 가져와 코드와 함께 소개해드리겠습니다.
# 예제로 사용할 주식 데이터 가져오기
!pip install finance-datareader
import pandas as pd
import FinanceDataReader as fdr
start_date = '20210101'
end_date = '20211231'
sample_code = '005930' # 삼성전자
stock = fdr.DataReader(sample_code, start = start_date, end = end_date)(1) Simple Moving Average
가장 먼저 소개해 드리는 방법은 단순 이동평균입니다. 단순 이동평균의 경우 주식투자 경험이 있으신 분이라면 한 번쯤은 접해보셨을 추세선입니다. 이는 구현 및 적용이 용이하나 적절한 파라미터 설정과 값이 우측으로 지연되는 특성이 있어 권하는 방법은 아닙니다.
def SMA(df, col, window=2):
return df[col].rolling(window=window, min_periods=1).mean()
stock['MA(5)'] = SMA(stock, 'Close', 5)
(2) Exponetial Moving Average
다음은 지수 이동평균입니다. 지수이동평균은 최근값에 가중치를 주며 이동평균을 계산합니다. 이때 평활 계수(EP = 2/(기간+1)를 사용하여 지수이동평균을 계산하게 됩니다. 지수이동평균 = (종가(t) x EP) + (지수 이동평균(t-1) x (1-EP))
def EMA(df, col, span=2):
return df[col].ewm(span=span).mean()
stock['EMA(5)'] = EMA(stock, 'Close', 5)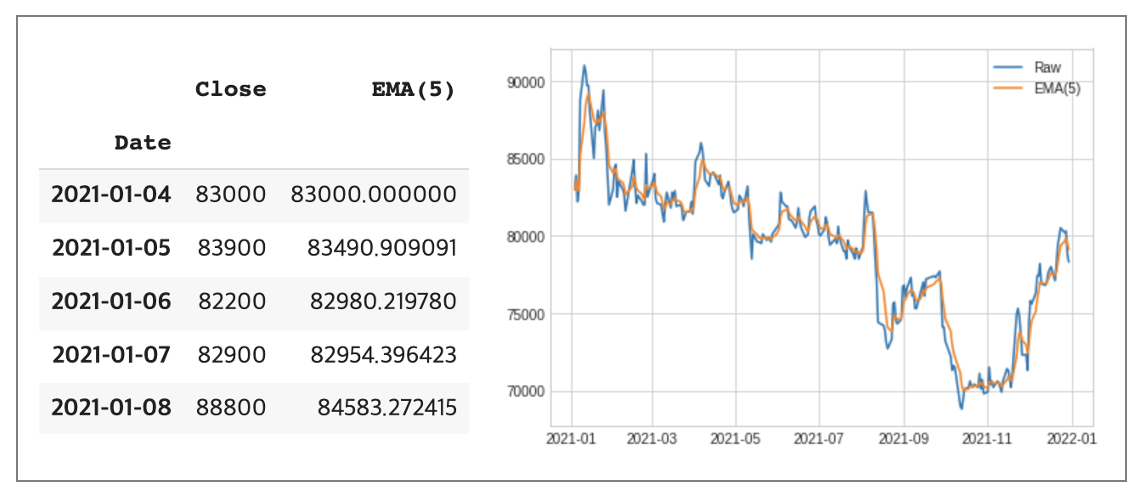
(3) Fourier Transform
다음은 푸리에 변환(Fourier Transform)입니다. 푸리에 변환은 이전 포스팅에서 설명드린 내용이며 푸리에는 어떤 복잡한 파동이라도 진동수와 진폭이 다른 간단한 파동들의 합으로 나타낼 수 있다는 것을 증명했습니다. 이를 잡음 제거에 활용하면 시간 차원에서 발생한 주식 종가 가격을 주파수 차원으로 변환하여 특정 상위 파동들의 합(예시에서는 상위 30개)을 계산하고 다시 시간 차원으로 변환합니다. 이를 통해 잡음을 제거하여 올바른 신호를 포착할 수 있습니다.
def FFT(df, col, topn=2):
fft = np.fft.fft(df[col])
fft[topn:-topn] = 0
ifft = np.fft.ifft(fft)
return ifft
stock['FFT(30)'] = FFT(stock, 'Close', 30)
복잡한 파동을 단순한 파동들의 합으로 표현하고 다시 시간차원으로 변환시키는 과정에서 시간축의 정보가 손실되기 때문에 우리는 해당 신호가 정확히 어느 시점에서 존재했는지 알 수 없습니다. 복잡한 신호일 수록 이런 단점이 더 부각되는데 이를 방지하고자 특정 시간 구간별로 푸리에 변환을 진행하는 STFT(Short Time Fourier Transform)이 소개되었습니다. 하지만 STFT 또한 특정 시간대(=window size)를 설정해야 하는데 이를 길게 잡으면 주파수의 해상도는 상승하지만 시간에 대한 해상도는 하락하고 이를 짧게 잡으면 주파수 해상도가 감소하고 시간에 대한 해상도는 상승합니다. 이와 같이 시간과 주파수 해상도에 대해 Trade-off 관계를 가지고 있어 사용에 유의하셔야 합니다. 본 포스팅에서는 STFT는 따로 코드 구현으로 활용하지 않겠습니다.(FFT 코드 활용하시면 쉽게 구현 가능합니다.)

(4) Wavelet Transform
다음은 웨이블릿 변환(Wavelet Transform)입니다. 웨이블릿 변환은 푸리에 변환의 단점을 해소하고자 개발되었고 고주파 성분 신호에 대해서는 주파수 해상도를 높이고 시간 해상도를 낮추는 한편 저주파 성분 신호에 대해서는 주파수 해상도를 낮추고 시간 해상도를 높이는 웨이블릿 함수를 사용합니다. 이렇듯 웨이블릿 변환은 시간의 확장과 축소하는 Scaling과 시간 축으로 이동되는 Shifting이 핵심입니다. 또한 동일한 자료를 분석하더라도 모 웨이블릿의 선택에 따라 결과가 달라지기 때문에 데이터 특성에 맞는 모 웨이블릿을 잘 선택해야하 하며 이산 웨이블릿 변환을 위해 Haar, Daubechies 등을 많이 사용합니다. 본 예제에서는 Daubechies를 사용하여 보여드리겠습니다.
def WT(df, col, wavelet='db5', thresh=0.63):
signal = df[col].values
thresh = thresh*np.nanmax(signal)
coeff = pywt.wavedec(signal, wavelet, mode="per" )
coeff[1:] = (pywt.threshold(i, value=thresh, mode="soft" ) for i in coeff[1:])
reconstructed_signal = pywt.waverec(coeff, wavelet, mode="per" )
return reconstructed_signal
(5) AutoEncoder
다음은 AutoEncoder입니다. 이전까지 설명드렸던 잡음 제거 방법들은 데이터 특성에 따라 분석가가 파라미터를 하나하나 설정해야 했습니다. 이런 파라미터를 결정하는데 많은 시간과 비용이 소비되기 때문에 종단 간(end-to-end) 딥러닝 모델로 잡음을 제거할 수 있는 응용모델(AutoEncoder,.. etc)을 예측 모델과 연결시켜 학습을 진행한다면 학습 비용을 감소시키면서 효과적으로 성능을 향상할 수 있습니다.
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torch.utils.data as data_utils
class TimeDistributed(nn.Module):
def __init__(self, module):
super(TimeDistributed, self).__init__()
self.module = module
def forward(self, x):
if len(x.size()) <= 2:
return self.module(x)
x_reshape = x.contiguous().view(-1, x.size(-1))
y = self.module(x_reshape)
if len(x.size()) == 3:
y = y.contiguous().view(x.size(0), -1, y.size(-1))
return y
class Autoencoder(nn.Module):
def __init__(self):
super(Autoencoder, self).__init__()
self.encoder = nn.LSTM(
input_size = 1,
hidden_size = 16,
dropout = 0.25,
num_layers = 2,
bias = True,
batch_first = True,
bidirectional = True,
)
self.decoder = nn.LSTM(
input_size = 32,
hidden_size = 16,
dropout = 0.25,
num_layers = 2,
bias = True,
batch_first = True,
bidirectional = True,
)
self.fc = TimeDistributed(nn.Linear(32, 1))
def forward(self, x):
h0, (h_n, c_n) = self.encoder(x)
h0, (h_n, c_n) = self.decoder(h0[:,-1:,:].repeat(1,5,1))
out = self.fc(h0)
return out
해당 방법들을 통해 재 생성된 데이터들의 정보와 잡음이 어떻게 분포되어 있는지 시각화 자료로 살펴보면, 단순 이동평균(MA)과 지수 이동평균(EMA)은 기존 데이터에 비해 스무딩 된 표현을 얻었습니다. 하지만 여전히 큰 분산을 보이고 있어 이를 활용 시 성능 향상에 도움이 될지 알 수 없습니다. 다음으로 푸리에 변환(FFT)을 살펴보면 기존 방법들에 비해 더 부드러운 표현을 가지게 되었고 많은 잡음이 제거된 것으로 보입니다. 웨이블릿 변환(WT)은 푸리에 변환보다 더 부드러운 파동의 형태를 지니게 되어 기존 잡음과 더불어 정보까지 같이 손실된 것처럼 보입니다. 이는 모 웨이블릿을 어떤 걸 사용하느냐에 따라 큰 차이가 발생할 수 있으므로 여러 실험을 통해 알맞은 함수를 찾아야 잡음 제거 효과를 얻을 수 있습니다. 마지막으로 오토 인코더(AE)의 경우 기존 데이터와 푸리에 변환 중간쯤의 표현력을 지닌 것으로 보입니다.

잡음 제거가 잘 되었는지 확인하는데 편차의 분포를 보는 것보다 예측 모델로 실험 결과를 보는 게 가장 정확하고 평가할 수 있습니다. 비교 결과 푸리에 변환(FFT)이 가장 좋은 성능을 지니고 있었고 그다음으로는 오토 인코더(AE) 모델이 잡음 제거로 인해 좋은 성능을 보이고 있습니다. 그에 반해 이동평균(MA, EMA) 방법들은 과거의 결과 자료로써 데이터를 재 구성하는 방법이기 때문에 후행 예측이 여전히 존재하고 있는 것을 눈으로 확인할 수 있었으며 검증 데이터의 학습이 제대로 진행되지 않는 것을 볼 수 있습니다. 웨이블릿 변환(WT)의 경우 후행 예측 문제를 해소할 수 있으나 변환 작업에서 신호의 잡음과 정보를 같이 손실되어 정확도를 잃게됐습니다. 하지만 예측 결과를 살펴보면 추세를 판단하기에 좋은 방법이라고 생각되어집니다.
| RAW | MA | EMA(5) | FFR(30) | WT(db5) | WT(db7) | WT(db9) | AE | |
| RMSE | 1,349(3) | 1,610 | 1,616 | 921(1) | 1,426 | 1,778 | 1,539 | 1,095(2) |
| MAE | 930(3) | 1,264 | 1,241 | 703(1) | 1,225 | 1,405 | 1,127 | 775(2) |
| MAPE | 1.23(3) | 1.67 | 1.64 | 0.93(1) | 1.61 | 1.85 | 1.48 | 1.02(2) |


금융 데이터는 자기 자신에 대해 영향을 미치는 자기 상관 특성이 강한 시계열 데이터입니다. 그렇기 때문에 이 데이터를 그대로 사용한다면 모델은 과거 데이터 속에 무시해야하는 무작위적 잡음을 분류해내지 못하고 실존하는 패턴과의 관계를 학습하지 못해 외삽(Extrapolate)해야할 진짜 패턴을 출력하지 못할것입니다. 그래서 우리는 모델에 데이터를 밀어줄 때 위와 같은 잡음 제거 방식을 사용해 올바른 정보만을 학습에 사용해야 합니다.
LESSONS LEARNED
이번 포스트에서는 잡음 제거(Denoising) 방식으로 데이터에서 쓸모있는 정보만 추출해 사용하여 기존 예측 모델에서 발생했던 후행 예측, 성능 저하, 잘못된 추론 등의 문제를 해결했습니다. 빅데이터 분석 업무를 수행하다보면 다양하고 대량의 데이터들을 빈번히 접하게 됩니다. 그리고 항상 이 데이터를 전달해주시는 분들은 데이터의 양이 충분하니 데이터에서 새로운 모멘텀을 얻길 기대하지만 이를 효과적으로 활용하는 방안들에 대해 고민해야할 일이 많습니다. 이번 포스트를 통해 같은 고민이 있으신 분들에게 도움이 됐으면 좋겠습니다.
'Data Science > 02_Time Series Analysis' 카테고리의 다른 글
| 시계열 데이터 이상 탐지(Anomaly Detection) (0) | 2022.05.23 |
|---|---|
| 시계열 데이터 예측 모델링(Stacked Hybrids) (1) | 2022.03.26 |
| 시계열 데이터 전처리(Encoding Time Step Features) (2) | 2022.01.31 |
| 다변량 선형 확률과정(VAR/Granger Causality/Cointegration) (1) | 2021.01.07 |
| 시계열 데이터 분석 싸이클 (0) | 2021.01.04 |