2022. 3. 26. 18:09ㆍData Science/02_Time Series Analysis

시계열 데이터는 패턴이 모두 동일하지 않으며 특성에 따라 매우 다양합니다. 도메인 지식이 있는 분야라면 이를 해석하고 분석하는데 큰 어려움이 없겠지만 그렇지 않다면 많은 시간을 소비하게 되고 정확한 예측 모델링이 어렵습니다. 이때 시계열 성분은 데이터 이해와 올바른 모델링을 하기 위한 가이드라인을 제시해줍니다.
TIME SERIES COMPONENT

시계열 데이터 성분은 추세(Trend), 계절성(Seasonality), 주기(Cycle), 잔차(Residual)로 이루어져 있습니다. 우선 추세란 단기~중기로 증가하거나 감소하는 패턴을 의미하며 주로 제품의 생명주기와 연관 지어 살펴볼 수 있습니다. 다음으로 계절성은 일, 주, 월, 년 단위로 변동이 반복적으로 관측되는 패턴을 의미하며 자연 현상이나 사회 규칙에서 주로 확인할 수 있습니다. 다음으로 주기는 계절성은 아니지만 증가하거나 감소하는 패턴을 나타낼 때 주로 보이며 정치나 경제 그리고 코로나 등 외부 요인으로 인해 발생합니다. 그리고 이 모든 시계열 성분을 제거하면 잔차가 남게 됩니다.
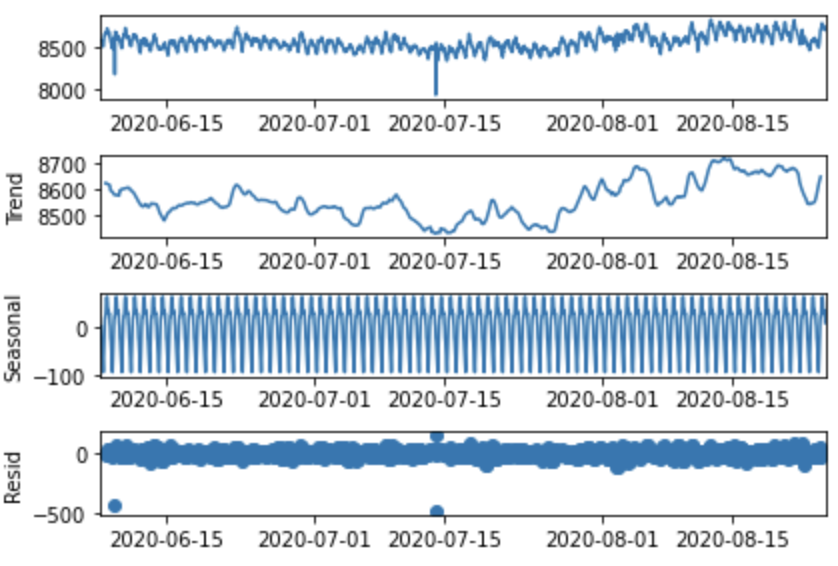
이와 같은 시계열 성분은 데이터 특징들을 더 직관적으로 이해할 수 있고 올바른 예측 모델링을 설계하는데 꼭 필요한 과정입니다. 예시를 통해 설명드리겠습니다.
MODEL DESIGN
우선 추세를 살펴보면 평가 데이터는 가장 최근의 데이터를 사용해야 미래 예측 시점의 분포와 가장 유사할 것으로 보입니다. 다음으로 계절성을 살펴보면 월요일에서 금요일로 갈수록 종가가 증가하는 패턴을 보이고 있어 모델에 학습 데이터를 최소 한 주 이상 밀어넣어줘야 모델이 패턴을 보다 잘 이해할 수 있을 것 같습니다. 그리고 주기를 보면 두번의 변곡점이 존재하는 것으로 보여 각 분포에 따른 모델을 별도로 만들어야 될 수도 있을 것 같습니다.

또한 증가하는 추세로 보아 예측해야 하는 시점은 과거에 보지 못한 값이 존재할 수 있을 것으로 보이며 이에 내삽(interpolation)이 아닌 외삽(extrapolation)가능한 모델을 선택해야 할 것입니다. 여기서 내삽이란 주어진 데이터 내에서 추론 가능한 것을 의미하며 트리 기반 예측 알고리즘은 대표적인 내삽만 가능한 모델입니다. 반대로 외삽은 주어진 데이터 외에서 추론 가능한 것을 의미하며 추세선을 학습하는 선형 모델 알고리즘들이 대표적인 외삽이 가능한 모델입니다.

그렇다면 위와 같은 시계열 데이터에는 외삽 가능한 모델만을 써야 하는 것일까?라는 의문이 드실 수 있습니다. 그에 대한 대답은 '아니요'입니다. 트리 기반 모델들은 변수간 상호작용(Interactions)을 보다 잘 학습하는 알고리즘이며 선형 기반 알고리즘은 특정 조건에 따른 추세를 보다 잘 학습하는 알고리즘입니다. 그래서 이번 포스팅에서는 서로의 약점을 보완하는 Stacked Hybrids 예측 모델링을 소개하고자 합니다.
STACKED HYBRIDS
예제를 위해 데이콘에서 진행되었던 전력사용량 예측 AI 경진대회 데이터를 가져왔습니다.
https://dacon.io/competitions/official/235736/data
전력사용량 예측 AI 경진대회 - DACON
좋아요는 1분 내에 한 번만 클릭 할 수 있습니다.
dacon.io
2020년 6월 1일 부터 2020년 8월 24일까지 데이터를 살펴보면 60개 건물들의 데이터가 시간 단위로 축적되어 있습니다. 간단히 구현해보기 위해 1개 건물에서 발생된 시간(time), 온도(temp), 풍속(wind), 습도(humidity)와 같은 설명변수와 실제 전력사용량(energy)인 종속변수만 가져와 데이터를 재 구성했습니다.
target = ['energy']
f_col = ['time', 'temp', 'wind', 'humidity']
train_x, test_x, train_y, test_y = train_test_split(
df[f_col],
df[target],
test_size=0.3,
shuffle=False,
)
train_x.head()
해당 데이터는 약 2달 동안의 짧은 시계열 데이터 이기 때문에 장기적으로 살펴보는 주기(Cycle)를 제외한 추세와 계절성만 살펴봤습니다. 우선 추세의 경우 다소 감소했다가 다시 증가하는 추이를 보이고 있으며 계절성의 경우 오전부터 증가하기 시작해 저녁에 감소하는 일 단위와 평일엔 다소 감소하는 주 단위로 나타나고 있습니다. 이와 같은 큰 변동이 없는 간단한 데이터는 트리 기반 부스팅 모델만을 사용해도 좋은 성능의 모델을 만들 수 있습니다.

하지만 우리가 학습시키는 데이터가 6월부터 8월까지만 존재하며 앞으로 예측해야 하는 시점의 전력 사용량이 증가하는 추세(여름 전력 사용량 증가)를 지니고 있다면 실제 전력량에 비해 과소 추정밖에 하지 못할 것입니다. 그래서 추세를 선형 회귀 모델로 먼저 학습시키고 시계열 데이터에 추세를 제거한 데이터(=계절성 패턴)를 트리 모델로 학습시켜 두 모델의 예측 결과를 합쳐 사용하면 문제를 해결할 수 있습니다. 이런 방법이 매우 기초적인 Stacked Hybrids 모델 구조입니다.
우선 시계열 데이터의 추세를 학습하기 위해 다항추세모형을 사용하겠습니다. 전력 사용량 데이터를 살펴보니 1차 추세로는 학습시키기 어려울 것으로 보이기 때문에 2차 추세 모형으로 학습시키겠습니다. 그림을 통해 학습 데이터로 추정한 추세선이 예측 데이터에도 잘 피팅 된걸 확인할 수 있습니다.
dp = DeterministicProcess(
index = train_x.index,
constant = True,
order = 2,
drop = True,
)
X = dp.in_sample()
lm = LinearRegression(fit_intercept=False)
lm.fit(X, train_y)
test_const = [1 for i in range(test_x.shape[0])]
test_trend = np.arange(X['trend'].max(), X['trend'].max()+test_x.shape[0])
test_trend_squared = [i**2 for i in test_trend]
X_ = pd.DataFrame([test_const, test_trend, test_trend_squared]).T
X_.columns = ['const', 'trend', 'trend_squared']
X_.index = test_x.index
trend_train = lm.predict(X)
trend_test = lm.predict(X_)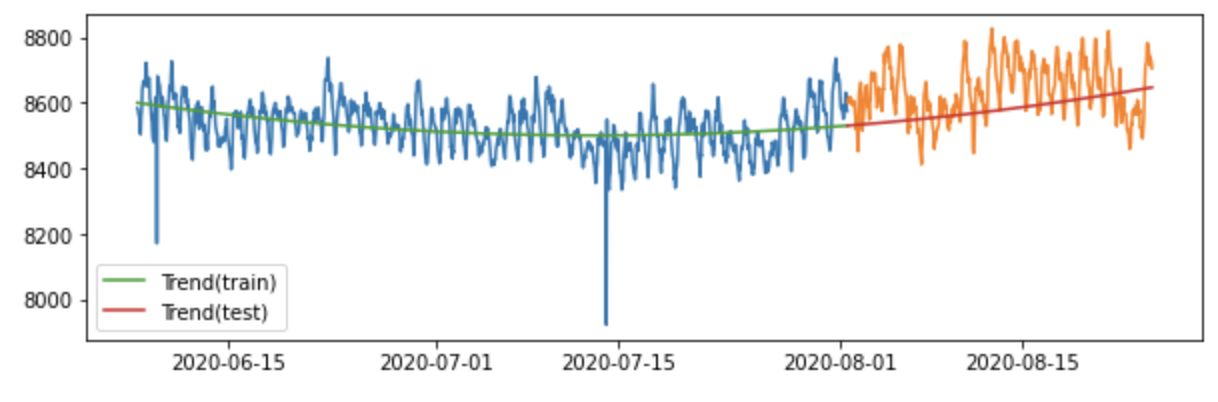
다음은 계절성을 XGB 모델을 사용하겠습니다. 이때 중요한것은 기존 설명변수들과 학습 데이터에서 추정한 추세를 제거한 데이터로 모델에 학습시켜야 합니다. 계절성 또한 그림을 통해 잘 학습된 것을 살펴볼 수 있습니다.
train_y_delta = train_y - trend_train
test_y_delta = test_y - trend_test
xgb= XGBRegressor()
xgb.fit(train_x, train_y_delta)
xgb_train = xgb.predict(train_x)
xgb_test = xgb.predict(test_x)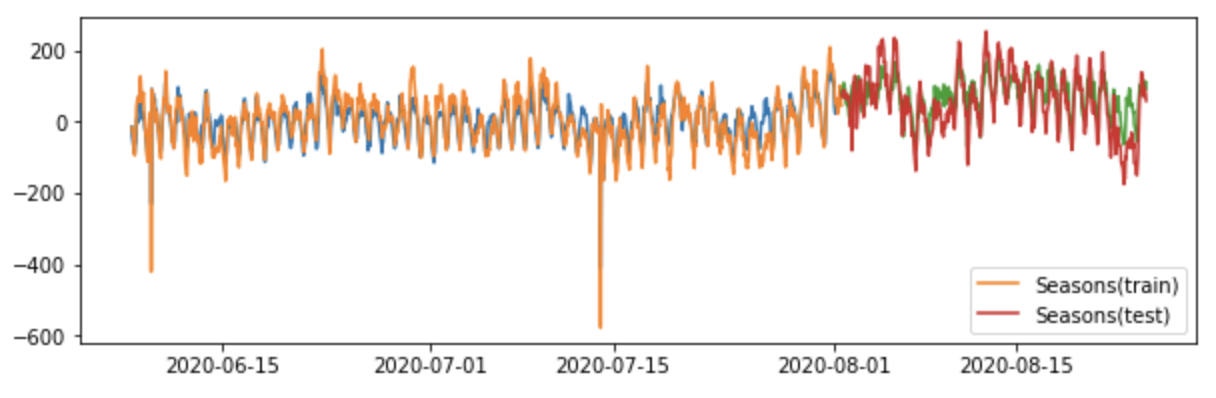
이제 Stacked Hybrids Model의 예측값은 추세 예측 값에 계절성 예측값을 더하면 됩니다. 2개의 모델 특징을 활용한 모델이 좋은 성능을 보여주는지 확인하기 위해 XGB 단일 모델로 학습한 결과와 비교해서 살펴보겠습니다. 평가 지표로는 MAE와 MAPE를 사용한 결과 Stacked Hybrids Model이 단일 XGB Model 보다 MAE, MAPE 모두 우수한 것을 확인했습니다.

LESSONS LEARNED
이번 포스팅을 작성하면서 최근에 본 '이상한 나라의 수학자' 최민식 배우님 말씀한 '잘못된 문제 정의는 올바른 답을 낼 수 없다' 란 대사가 생각났습니다. 머신러닝 모델링 과정 또한 이와 똑같다고 생각합니다. 종속 변수를 보다 잘 설명할 수 있는 변수를 찾거나 SOTA 알고리즘을 적용해 높은 성능을 만드는 게 아니라 제대로 된 문제를 정의하는 게 보다 중요하다고 생각합니다. 그리고 이런 문제를 정의하기 위해서는 문제의 속성을 이해해야 하며 이 과정이 선행되어야 현실과의 차이를 최소한으로 줄여 제대로 된 문제를 마주하게 될 수 있을 것입니다.
'Data Science > 02_Time Series Analysis' 카테고리의 다른 글
| 시계열 데이터 이상 탐지(Anomaly Detection) (0) | 2022.05.23 |
|---|---|
| 시계열 데이터 전처리(Denoising Method) (7) | 2022.02.13 |
| 시계열 데이터 전처리(Encoding Time Step Features) (2) | 2022.01.31 |
| 다변량 선형 확률과정(VAR/Granger Causality/Cointegration) (1) | 2021.01.07 |
| 시계열 데이터 분석 싸이클 (0) | 2021.01.04 |