시계열 데이터 전처리3
2020. 12. 16. 10:35ㆍData Science/02_Time Series Analysis
반응형
종속변수의 정상성 이해하기
: 시계열 데이터 전처리의 마지막으로 종속변수의 정상성을 살펴봄
1. 정상성
: 시간이 흐름에 따라 "통계적 특성(Stastistical Properties)"이 변하지 않음을 정상이이 있다라고 표현
: "통계적 특성(Stastistical Properties)"이란 모멘텀이라 해서 수학적으로 n차 미분했을 때 통계적 특징(평균, 분산, 공분산 등)
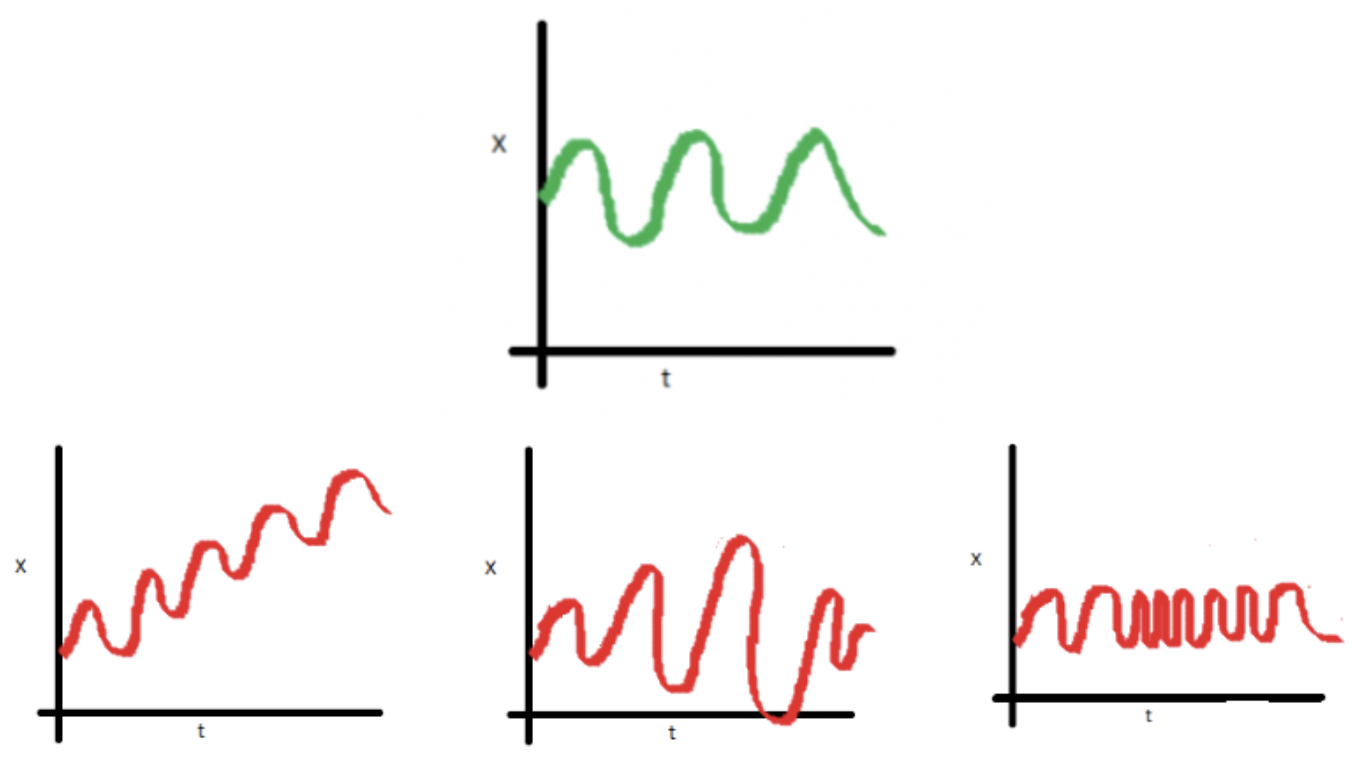
2. 약정상
: 일반적인 정상성을 의미함
: 비 수학적 이해
- 𝑋𝑖1Xi1, 𝑋𝑖2Xi2, 𝑋𝑖3Xi3, ... have the same distribution.
- (𝑋𝑖1,𝑋𝑖3)(Xi1,Xi3), (𝑋𝑖5,𝑋𝑖7)(Xi5,Xi7), (𝑋𝑖9,𝑋𝑖11)(Xi9,Xi11), ... have the same joint distribution. That's it.
: 수학적 이해
- 𝐸(𝑋𝑖𝑡)=𝜇E(Xit)=μ, for all time 𝑡t (The first moment estimation)
- 𝑉𝑎𝑟(𝑋𝑖𝑡)=𝐸(𝑋2𝑖𝑡)−𝐸(𝑋𝑖𝑡)2<∞Var(Xit)=E(Xit2)−E(Xit)2<∞, for all time 𝑡t (The second moment estimation)
- 𝐶𝑜𝑣(𝑋𝑖𝑠,𝑋𝑖𝑘)=𝐶𝑜𝑣(𝑋𝑖(𝑠+ℎ),𝑋𝑖(𝑘+ℎ))=𝑓(ℎ)Cov(Xis,Xik)=Cov(Xi(s+h),Xi(k+h))=f(h), for all time 𝑠,𝑘,ℎs,k,h (The cross moment estimation)
3. 강정상
: 확률과정의 모든 분포 모멘트(Moment)가 시간 차이에만 의존하는 것(절대시간 미의존)
: 비 수학적 이해
- 𝑋𝑖1Xi1, 𝑋𝑖2Xi2, 𝑋𝑖3Xi3, ... have the same distribution.
- (𝑋𝑖1,𝑋𝑖3)(Xi1,Xi3), (𝑋𝑖5,𝑋𝑖7)(Xi5,Xi7), (𝑋𝑖9,𝑋𝑖11)(Xi9,Xi11), ... have the same joint distribution.
- (𝑋𝑖1,𝑋𝑖3,𝑋𝑖5)(Xi1,Xi3,Xi5), (𝑋𝑖7,𝑋𝑖9,𝑋𝑖11)(Xi7,Xi9,Xi11), (𝑋𝑖13,𝑋𝑖15,𝑋𝑖17)(Xi13,Xi15,Xi17), ... must have the same joint distribution.
- (𝑋𝑖1,𝑋𝑖3,...,𝑋𝑖∞)(Xi1,Xi3,...,Xi∞) is invariant under all time translation.
: 백색잡음(White Noise, W N)는 강정상의 예시로 시계열분석 기본알고리즘 중 가장 중요함
: 잔차들은 1)정규분포이며, 2)평균과 일정한 분산을 가져야하고, 3)시간의 흐름에 따라 상관성이 없어야 함

4. 랜덤 워크(Random Walk)
: 추세가 있어서 일차 모멘트가 0이 아니며 시간에 따라 변화함
: 비정상 데이터의 가장 기초적인 예시
: 𝑌𝑖𝑡=𝑌𝑖𝑡−1+𝜖𝑡 => 𝑌𝑖𝑡−𝑌𝑖𝑡−1=𝜖𝑡 => 𝜖𝑡∼𝑊𝑁(0,𝜎2𝜖𝑡)

반응형
'Data Science > 02_Time Series Analysis' 카테고리의 다른 글
| 시계열 알고리즘_AR/MA/ARMA (0) | 2020.12.18 |
|---|---|
| 정규화(Regularization)/배깅(Bagging)/부스팅(Boosting) (0) | 2020.12.17 |
| 시계열 데이터 전처리2 (0) | 2020.12.15 |
| 잔차 진단 (0) | 2020.12.14 |
| 시계열 데이터 전처리1 (0) | 2020.12.10 |